kodaskola

Tarjana algoritms

---

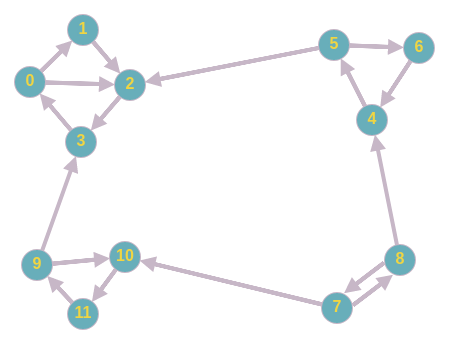
Tarjana algoritms ir uz dfs bāzēts algoritms, kurš atrod cieši saistītas komponentes orientētā grafā.

Katrai virsotnei glabā 3 vērtības:

• index - unikāls indeks, kurš tiek piešķirts pieaugošā secībās, apstaigājot grafu.
• link - indeks, kurš norāda pašreiz apstaigātajā ceļā virsotni ar zemāko indeksu, ar kuru veidojas cikls.
• onStack - apzīmē vai virsotne ir pašreiz apstaigātajā ceļā, kuru glabā stekā.

Rekursīvu dfs veic uz katru vēl neapskatīto virsotni. Sākot apskatīt virsotni u, tai piešķir jaunu indeksu, kurš ir lielāks par visiem iepriekš piešķirtajiem un atzīmē, ka zemākais indeks ar kuru veidojas cikls ir šī pati virsotne. Ieliek virsotni u stekā, kurā glabājas pašreizējajā rekursīvajā ceļā apskatītās virsotnes.

Tālāk iet cauri visām virsotnes kaimiņu virsotnēm v. Ja kāda no tām nav apskatīta, rekursīvi to apskata. Pēc atgriešanās no rekursijas pārbauda, vai gadījumā virsotne v neveido ciklu ar kādu virsotni, kuras indeks ir mazāks, nekā u virsotnes mazākais ciklu veidojošais indekss:

G[u].link = min(G[u].link, G[v].link);

Savukārt, ja virsotne jau ir apskatīta, bet tā atrodas pašreizējajā apskatāmajā ceļā, tad pārbauda, tad tā veido ciklu, kur virsotnes v indeks būs mazākais šī cikla indeks, tāpēc pārbauda vai u virsotnes mazāko ciklu veidojošo indeksu ir iespējams uzlabot

G[u].link = min(G[u].link, G[v].index);

Kad visas kaimiņu virsotnes ir apskatītas, atliek pārbaudīt, ja esošās virsotnes u mazākais ciklu veidojošās virsotnes indekss (link) ir vienāds ar pašu virsotni, tas nozīmē, ka stekā līdz pat šai virsotnei, visas virsotnes ir iekļautas ciklā un tāpēc veido saistītu komponenti.

#include <bits/stdc++.h>

using namespace std;

#define N 1000

struct Vertex {
    int index, link;
    bool onStack;
    vector<int> adj;
};

Vertex G[N];

int lastIndex;
stack<int> S;

vector<vector<int> > res;

void tarjanRec(int u) {
    lastIndex++;
    G[u].index = lastIndex;
    G[u].link = lastIndex;
    G[u].onStack = true;
    S.push(u);

    for(auto v:G[u].adj) {
        if (G[v].index == 0) {
            tarjanRec(v);
            G[u].link = min(G[u].link, G[v].link);
        } else if (G[v].onStack) {
            G[u].link = min(G[u].link, G[v].index);
        }
    }

    // virsotne, kura ir ar mazāko indeksu saistītā komponenetē
    if (G[u].index == G[u].link) {
        vector<int> V;
        int v = -1;
        while (v != u) {
            v = S.top();
            S.pop();
            G[v].onStack = false;
            V.push_back(v);
        }
        res.push_back(V);
    }

}

void tarjan(int n) {
    for(int i = 0; i < n; i++) {
        if (G[i].index == 0) tarjanRec(i);
    }
}


int main()
{
    int edges[17][2] = {
        {0, 1}, {0, 2}, {1, 2}, {2, 3}, {3, 0},
        {4, 5}, {5, 2}, {5, 6}, {6, 4},
        {7, 8}, {7, 10}, {8, 4}, {8, 7},
        {9, 3}, {9, 10}, {10, 11}, {11, 9}};
    // no virsotnēm izveido grafu
    for(int i = 0; i < 17; i++) {
        G[edges[i][0]].adj.push_back(edges[i][1]);
    }

    int n = 12;

    tarjan(n);

    for(auto V:res) {
        for(auto u:V) {
            cout << u << " ";
        }
        cout << endl;
    }
}